Section: New Results

Formal Verification of a Synchronous Data-flow Compiler: from Signal to C

Participants : Van-Chan Ngo, Jean-Pierre Talpin, Thierry Gautier, Paul Le Guernic, Loïc Besnard.

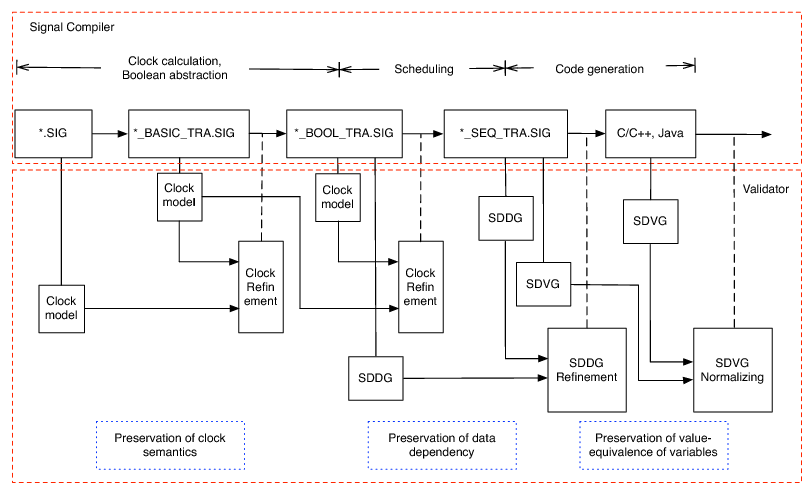
Translation validation (Translation validation. Pnueli A., Siegel M., and Singerman E. In Proceedings of TACAS'98, 1998.) (Translation validation: From signal to c. M. Siegel A. Pnueli and E. Singeman. In Correct Sytem Design Recent Insights and Advances, 2000.) is a technique that attempts to verify that program transformations preserve the program semantics. It is obvious to prove globally that the source program and its final compiled program have the same semantics. However, we believe that a better approach is to separate concerns and prove each analysis and transformation stage separately with respect to ad-hoc data-structures to carry the semantic information relevant to that phase.

In the case of the Signal compiler [1] , [7] [12] , the preservation of the semantics can be decomposed into the preservation of clock semantics at the clock calculation phase and that of data dependencies at the static scheduling phase, and, finally, value-equivalence of variables at the code generation phase.

Translation Validation for Clock Transformations in a Synchronous Compiler. In this work, the clock semantics of the source and transformed programs are formally represented as clock models. A clock model is a first-order logic formula that characterizes the presence/absence status of all signals in a Signal program at a given instant. Given two clock models, a clock refinement between them is defined which expresses the semantic preservation of clock semantics. A method to check the existence of clock refinement is defined as a satisfiability problem which can be automatically and efficiently proved by a SMT solver.

Let $C{p}^{sig}$ and $Va{l}_{clk}$ be the functions which define the Signal compiler and a validator, respectively. The following function defines a formally verified compiler for the clock calculation and Boolean abstraction phase. We write $C{⊑}_{clk}A$ to denote that there exists a refinement between $A$ and $C$.

where $Va{l}_{clk}(A,C)=$ true if and only if $C{⊑}_{clk}A$.

Precise Deadlock Detection for Polychronous Data-flow Specifications. Dependency graphs are a commonly used data structure to encode the streams of values in data-flow programs and play a central role in scheduling instructions during auto-mated code generation from such specifications. In this work [17] , we propose a precise and effective method that combines a structure of dependency graph and first order logic formulas to check whether multi-clocked data-flow specifications are deadlock free before generating code from them. We represent the flow of values in the source programs by means of a dependency graph and attach first-order logic formulas to condition these dependencies. We use an SMT solver (Satisfiability modulo theories: An appetizer. L. de Moura and N. Bjorner. In Brazilian Symposium on Formal Methods, 2009.) to effectively reason about the implied formulas and check deadlock freedom.

Evaluating SDVG translation validation: from Signal to C. This work focuses on proving that every output signal in the source program and the corresponding variable in the compiled program, the generated C program, have the same values. The computations of all signals and their compiled counterparts are represented by a shared value-graph, called Synchronous Data-flow Value-Graph (SDVG).

Given a SDVG, assume that we want to show that two variables have the same value. We simply need to check that they are represented by the same sub-graph, meaning that they point to the same graph node. If all output signals in the source program $A$ and the corresponding variables in the generated $C$ program have the same value, then we say that $C$ refines $A$, denoted by $C{⊑}_{val}A$.

Implementation and Experiments. At a high level, our tool SigCert (https://scm.gforge.inria.fr/svn/sigcert ) developed in OCaml checks the correctness of the compilation of Signal compiler w.r.t clock semantics, data dependence, and value-equivalence as given in Figure 3 .