Section: Research Program
Computational fluid mechanics: modeling or not before discretizing ?
A typical continuous solution of the Navier Stokes equations at sufficiently high values of the Reynolds number is governed by a spectrum of time and space scales fluctuations closely connected with the turbulent nature of the flow. The term deterministic chaos employed by Frisch in its enlightening book [33] is certainly conveying most adequately the difficulty in analyzing and simulating this kind of flows. The broadness of the turbulence spectrum is directly controlled by the Reynolds number defined as the ratio between the inertial forces and the viscous forces. This number is not only useful to determine the transition from a laminar to a turbulent flow regime, it also indicates the range of scales of fluctuations that are present in the flow under consideration.
Typically, for the velocity field and far from solid walls, the ratio between the largest scale (the integral length scale) to the smallest one (Kolmogorov scale) scales as per dimension. In addition, for internal flows, the viscous effects near the solid walls yield a scaling proportional to per dimension. The smallest scales play a crucial role in the dynamics of the largest ones which implies that an accurate framework for the computation of turbulent flows must take into account all these scales.
Thus, the usual practice to deal with turbulent flows is to choose between an a priori modeling (in most situations) or not (low Re number and rather simple configurations) before proceeding to the discretization step followed by the simulation runs themselves. If a modeling phase is on the agenda, then one has to choose again among the above mentioned variety of approaches.
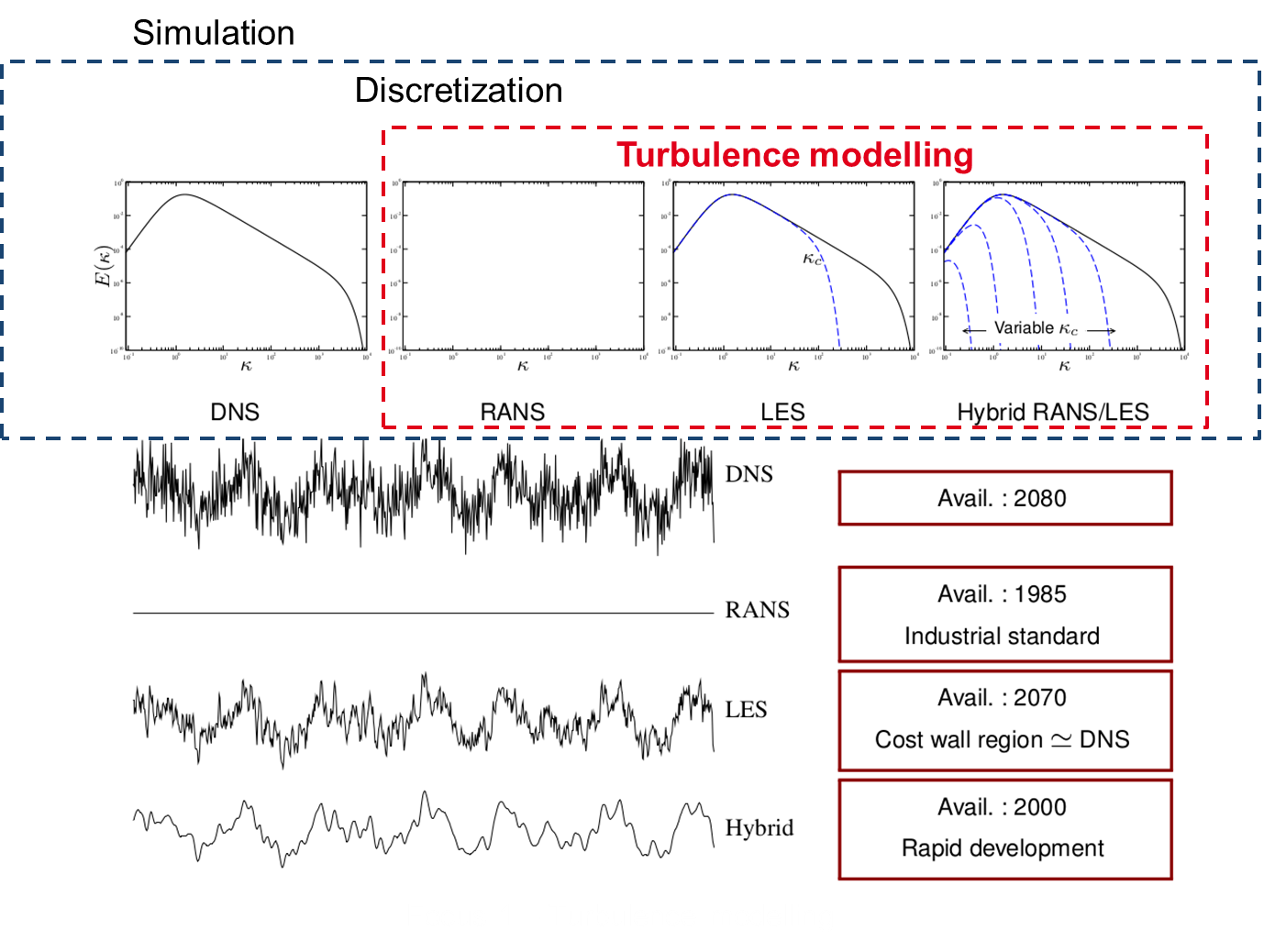
As it is illustrated in Fig. 1 , this can be achieved either by directly solving the Navier-Stokes equations (DNS) or by first applying a statistical averaging (RANS) or a spatial filtering operator to the Navier-Stokes equations (LES). The new terms brought about by the filtering operator have to be modeled. From a computational point of view, the RANS approach is the least demanding, which explains why historically it has been the workhorse in both the academic and the industrial sectors. It has permitted quite a substantial progress in the understanding of various phenomena such as turbulent combustion or heat transfer. Its inherent inability to provide a time-dependent information has led to promote in the last decade the recourse to either LES or DNS to supplement if not replace RANS. By simulating the large scale structures while modeling the smallest ones supposed to be more isotropic, LES proved to be quite a step through that permits to fully take advantage of the increasing power of computers to study complex flow configurations. At the same time, DNS was progressively applied to geometries of increasing complexity (channel flows with values of multiplied by 10 during the last 15 years, jets, turbulent premixed flames, among many others), and proved to be a formidable tool that permits (i) to improve our knowledge on turbulent flows and (ii) to test (i.e., validate or invalidate) and improve the modeling hypotheses inherently associated to the RANS and LES approaches. From a numerical point of view, if the steady nature of the RANS equations allows to perform iterative convergence on finer and finer meshes, the high computational cost of LES or DNS makes necessary the use of highly accurate numerical schemes in order to optimize the use of computational resources.
To the noticeable exception of the hybrid RANS-LES modeling, which is not yet accepted as a reliable tool for industrial design, as mentioned in the preamble of the Go4hybrid European program (http://www.transport-research.info/web/projects/project_details.cfm?id=46810 ), once chosen, a single turbulence model will (try to) do the job for modeling the whole flow. Thus, depending on its intrinsic strengths and weaknesses, the accuracy will be a rather volatile quantity strongly dependent on the flow configuration. The turbulence modeling and industrial design communities waver between the desire to continue to rely on the RANS approach, which is unrivaled in terms of computational cost, but is still not able to accurately represent all the complex phenomena; and the temptation to switch to LES, which outperforms RANS in many situations but is prohibitively expensive in high-Reynolds number wall-bounded flows. In order to account for the deficiencies of both approaches and to combine them for significantly improving the overall quality of the modeling, the hybrid RANS-LES approach has emerged during the last decade as a viable, intermediate way, and we are definitely inscribing our project in this innovative field of research, with an original approach though, connected with a time filtered hybrid RANS-LES and a systematic and progressive validation process against experimental data produced by the team.
|