Section: New Results

Approximation

Isotopic approximation within a tolerance volume

Participants : Manish Mandad, Pierre Alliez.

In collaboration with David Cohen-Steiner from the GEOMETRICA project-team.

We introduce an algorithm that generates a surface triangle mesh given an input tolerance volume. The mesh is guaranteed to be within the tolerance, intersection free and topologically correct. A pliant meshing algorithm is used to capture the topology and discover the anisotropy in the input tolerance volume in order to generate a concise output. We first refine a 3D Delaunay triangulation over the tolerance volume while maintaining a piecewise-linear function on this triangulation, until an isosurface of this function matches the topology sought after. We then embed the isosurface into the 3D triangulation via mutual tessellation, and simplify it while preserving the topology. Our approach extends to surfaces with boundaries and to non-manifold surfaces. We demonstrate the versatility of our approach on a variety of data sets and tolerance volumes [7] . Figure 10 illustrates the robustness of our approach on defect-laden inputs.

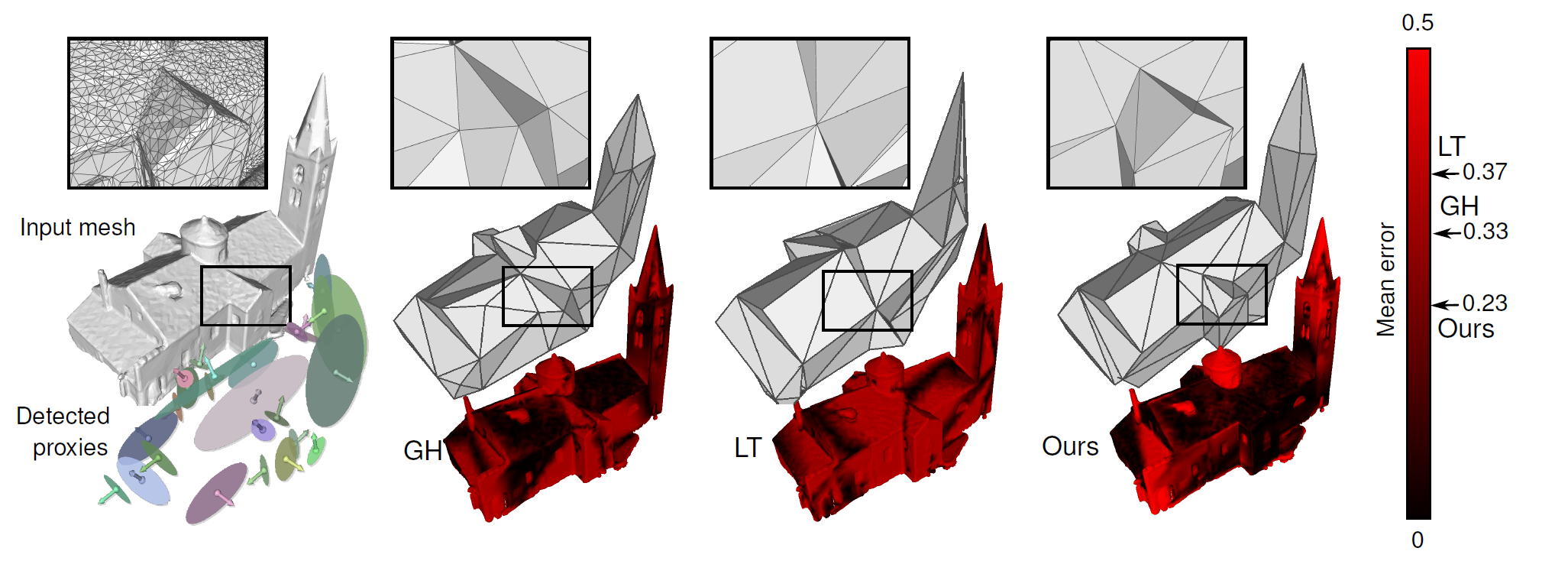
Structure-Aware Mesh Decimation

Participants : David Salinas, Florent Lafarge, Pierre Alliez.

We contributed to a novel approach for the decimation of triangle surface meshes. Our algorithm takes as input a triangle surface mesh and a set of planar proxies detected in a pre-processing analysis step, and structured via an adjacency graph. It then performs greedy mesh decimation through a series of edge collapse operators, designed to approximate the local mesh geometry as well as the geometry and structure of proxies (Figure 11 ). Such structure-preserving approach is well suited to planar abstraction, i.e., extreme decimation approximating well the planar parts while filtering out the others. Our experiments on a variety of inputs illustrate the potential of our approach in terms of improved accuracy and preservation of structure [9] .

CGALmesh: a Generic Framework for Delaunay Mesh Generation

Participants : Clément Jamin, Pierre Alliez.

In collaboration with Mariette Yvinec and Jean-Daniel Boissonnat from the GEOMETRICA project-team.

CGALmesh is the mesh generation software package of the Computational Geometry Algorithm Library (CGAL). It generates isotropic simplicial meshes – surface triangular meshes or volume tetrahedral meshes – from input surfaces, 3D domains as well as 3D multi-domains, with or without sharp features (see Figure 12 ). The underlying meshing algorithm relies on restricted Delaunay triangulations to approximate domains and surfaces, and on Delaunay refinement to ensure both approximation accuracy and mesh quality. CGALmesh provides guarantees on approximation quality as well as on the size and shape of the mesh elements. It provides four optional mesh optimization algorithms to further improve the mesh quality. A distinctive property of CGALmesh is its high flexibility with respect to the input domain representation. Such a flexibility is achieved through a careful software design, gathering into a single abstract concept, denoted by the oracle, all required interface features between the meshing engine and the input domain. We already provide oracles for domains defined by polyhedral and implicit surfaces [6] .