Section: Research Program
Numerical methods for real-time simulation
Objectives:
-
Context-aware discretization and adaptive (re)meshing for cuts and fractures
-
Advanced constraints: Interaction, multi-body contacts - Collision detection
Milestones:
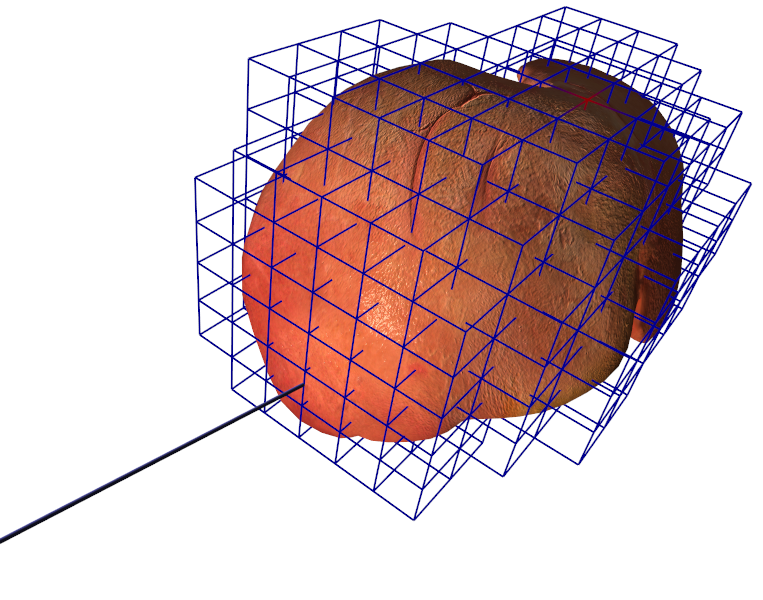
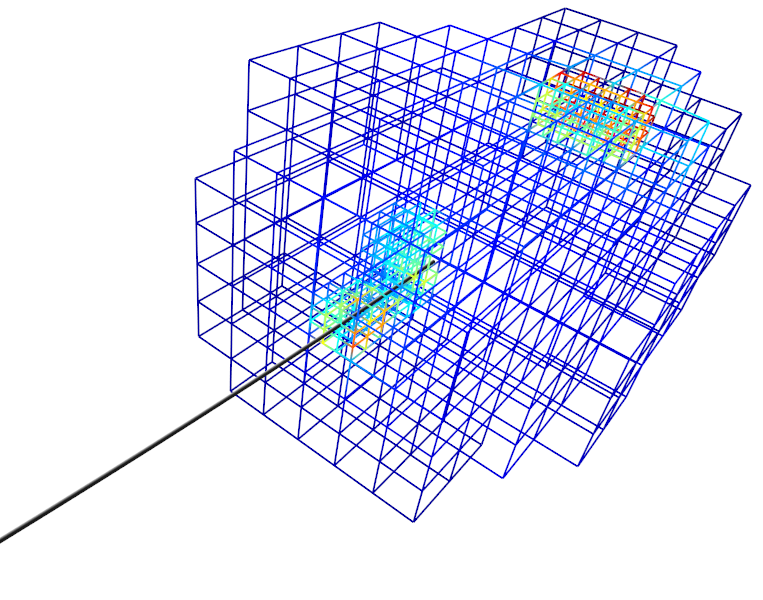
The principal objective of this second challenge is to improve, at the numerical level, the efficiency, robustness, and quality of the simulations. To reach these goals, we essentially rely on two approaches: adaptive meshing to allow mesh transformations during a simulation and support cuts, local remeshing or dynamic refinement in areas of interest; and numerical techniques, such as asynchronous solvers, domain decomposition and model order reduction (Figure 3).
Typically, the simulations in the field of biomechanics, physiological modeling, or even computer graphics, employ techniques based on the finite element method. Such simulations require a discretization of the domain of interest, and this discretization is traditionally made of tetrahedral or hexahedral elements. The topology defined by these elements is also considered constant. The first objective of this work is to jointly develop advanced topological operations and new finite element approaches that can leverage the use of dynamic topologies. In particular we focus our research on multi-resolution meshes where elements are subdivided in areas where numerical errors need to be kept small [25], [27].
|
Once the problem, as defined in the previous challenge, has been discretized, we need to solve a large system of linear or nonlinear equations. In both cases, it is necessary to employ numerical solvers repeatedly to construct the solution representing the state of the simulated system. In the past years, we have contributed to this topic through our work on asynchronous preconditioning [19]. We would like to pursue this area of research exploiting the relevant advances in hierarchy-based topologies (e.g. the multi-grid methods). We will also consider advanced non-linear solvers which are necessary for correct resolution of hyper-elastic models and composite models.
Finally, to improve computational times from a programming stand-point, we have started a collaboration with the CAMUS team at Inria. This collaboration aims at using smart code analysis and on-the-fly parallelism to automatically speed-up computation times. In a typical scenario, the modeled organ or tissue is surrounded by its environment represented by other organs, connective tissues or fat. Further, during the intervention, the tissues are manipulated with instruments. Therefore, the interaction will also be an important aspect of our research. We have already developed methods for modeling of advanced interactions between organs, tissues and tools [24] [20]. We will continue exploiting novel methods such as partial factorization [28] and integrate our approach with other techniques such as augmented Lagrangian.