Section: New Results
Dictionary Learning for Massive Matrix Factorization
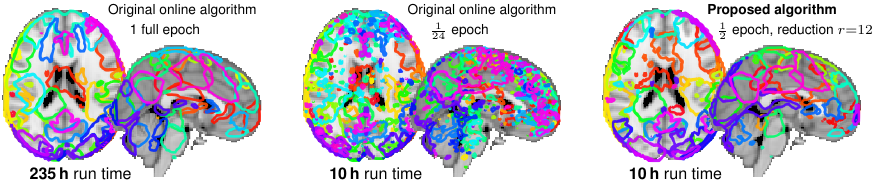
Sparse matrix factorization is a popular tool to obtain interpretable data decompositions, which are also effective to perform data completion or denoising. Its applicability to large datasets has been addressed with online and randomized methods, that reduce the complexity in one of the matrix dimension, but not in both of them. In this paper, we tackle very large matrices in both dimensions. We propose a new factoriza-tion method that scales gracefully to terabyte-scale datasets, that could not be processed by previous algorithms in a reasonable amount of time. We demonstrate the efficiency of our approach on massive functional Magnetic Resonance Imaging (fMRI) data, and on matrix completion problems for recommender systems, where we obtain significant speed-ups compared to state-of-the art coordinate descent methods.
|
See Fig. 3 for an illustration and [22] for more information.