Section: New Results

Statistical methods for image denoising and reconstruction

Participants : Emmanuel Moebel, Charles Kervrann.

In the line of the Non-Local (NL) means [39] and ND-SAFIR [11], [12], [6] denoising algorithms, we have proposed a novel adaptive estimator based on the weighted average of observations taken in a neighborhood with weights depending on image data. The idea is to compute adaptive weights that best minimize an upper bound of the pointwise $L_2$ risk. In the framework of adaptive estimation, we show that the “oracle” weights depend on the unknown image and are optimal if we consider triangular kernels instead of the commonly-used Gaussian kernel. Furthermore, we propose a way to automatically choose the spatially varying smoothing parameter for adaptive denoising. Under conventional minimal regularity conditions, the obtained estimator converges at the usual optimal rate. The implementation of the proposed algorithm is also straightforward. The simulations show first that our algorithm improves significantly the classical NL-means. Second, the simulations demonstrate that it is competitive when compared to state-of-the-art denoisers both in terms of PSNR values and visual quality.

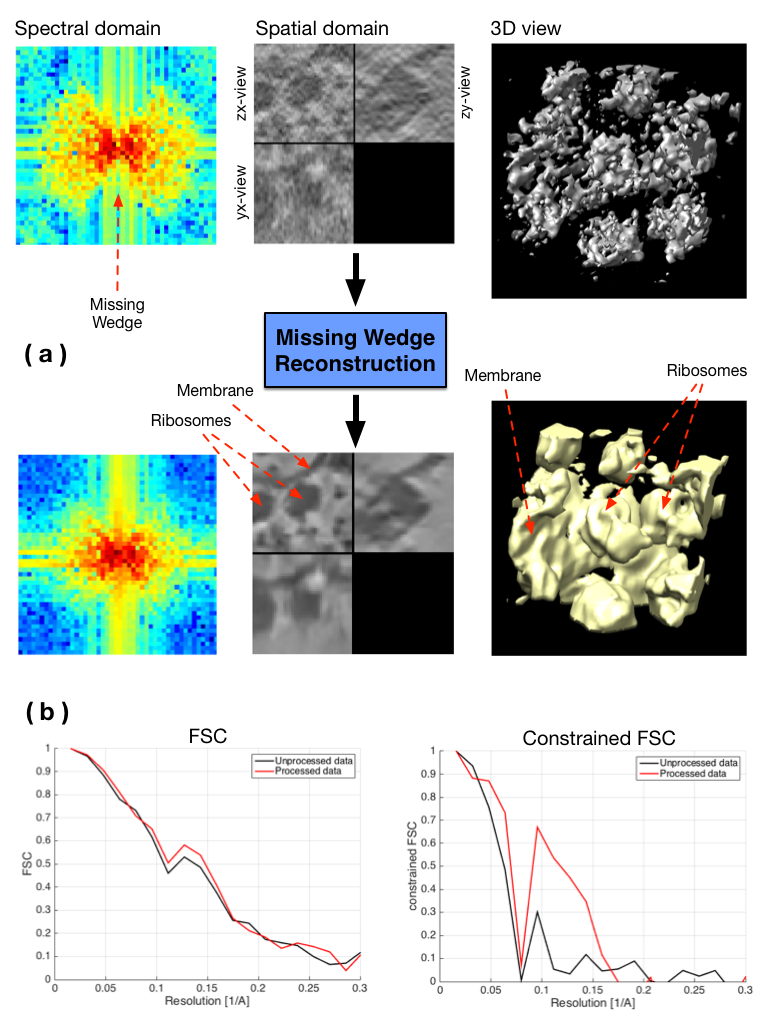
Meanwhile, we investigated statistical aggregation methods which optimally combine several estimators to produce a boosted solution [13]. This approach has been especially investigated to restore spectral information in the missing wedge (MW) in cryo-electron tomography (CET). The MW is known to be responsible for several types of imaging artifacts, and arises because of limited angle tomography: it is observable in the Fourier domain and is depicted by a region where Fourier coefficient values are unknown (see Fig. 3). The proposed stochastic method tackles the restoration problem by filling up the MW by iterating following steps: adding noise into the MW (step 1) and applying a denoising algorithm (step 2). The role of the first step is to propose candidates for the missing Fourier coefficients and the second step acts as a regularizer. A constraint is added in the spectral domain by imposing the known Fourier coefficients to be unchanged through iterations. Different denoising algorithms (BM3D, NL-Bayes, NL-means...) have been compared. Furthermore, different transforms have been tested in order to apply the constraint (Fourier transform, Cosine transform, pseudo-polar Fourier transform). Finally, we showed that this strategy can be embedded into a Monte-Carlo simulation framework and amounts to computing an aggregated estimator [13]. Convincing results have been achieved (see Fig. 3) using the Fourier Shell Correlation (FSC) as an evaluation metric.

References:  [18]

Collaborators: Qiyu Jin (School of Mathematical Science, Inner Mongolia University, China),

                          Ion Grama and Quansheng Liu (University of Bretagne-Sud, Vannes),

                          Damien Larivière (Fondation Fourmentin-Guilbert),

                          Julio Ortiz (Max-Planck Institute, Martinsried, Germany).