Section: New Results

Large-scale Optimization for Machine Learning

Stochastic Subsampling for Factorizing Huge Matrices

Participants : Julien Mairal, Arthur Mensch [Inria, Parietal] , Gael Varoquaux [Inria, Parietal] , Bertrand Thirion [Inria, Parietal] .

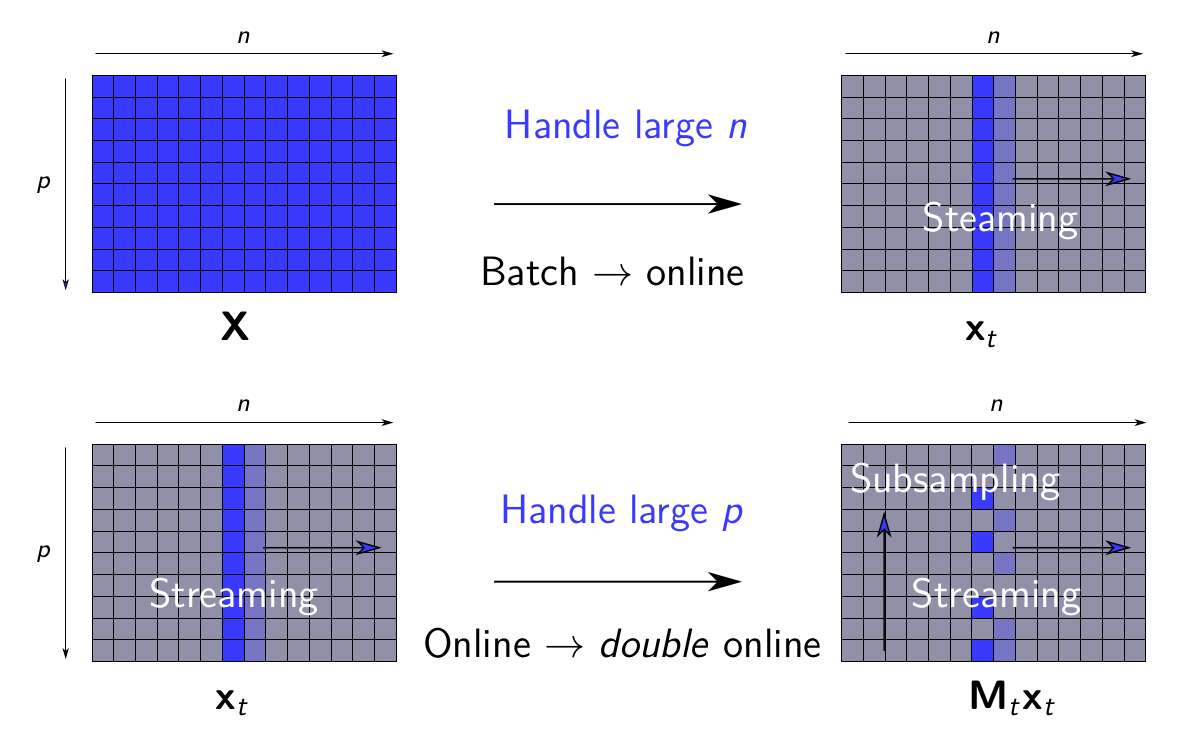
In [10], we present a matrix-factorization algorithm that scales to input matrices with both huge number of rows and columns. Learned factors may be sparse or dense and/or non-negative, which makes our algorithm suitable for dictionary learning, sparse component analysis, and non-negative matrix factorization. Our algorithm streams matrix columns while subsampling them to iteratively learn the matrix factors. At each iteration, the row dimension of a new sample is reduced by subsampling, resulting in lower time complexity compared to a simple streaming algorithm. Our method comes with convergence guarantees to reach a stationary point of the matrix-factorization problem. We demonstrate its efficiency on massive functional Magnetic Resonance Imaging data (2 TB), and on patches extracted from hyperspectral images (103 GB). For both problems, which involve different penalties on rows and columns, we obtain significant speed-ups compared to state-of-the-art algorithms. The main principle of the method is illustrated in Figure 19.

An Inexact Variable Metric Proximal Point Algorithm for Generic Quasi-Newton Acceleration

Participants : Hongzhou Lin, Julien Mairal, Zaid Harchaoui [Univ. Washington] .

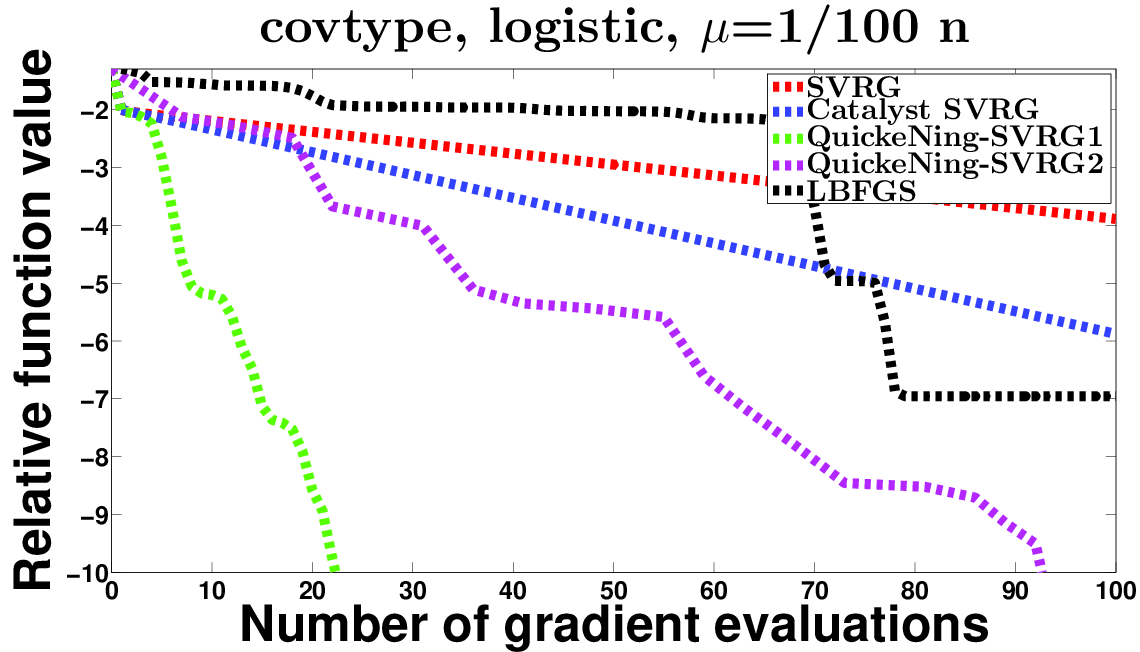
In [43], we propose a generic approach to accelerate gradient-based optimization algorithms with quasi-Newton principles. The proposed scheme, called QuickeNing, can be applied to incremental first-order methods such as stochastic variance-reduced gradient (SVRG) or incremental surrogate optimization (MISO). It is also compatible with composite objectives, meaning that it has the ability to provide exactly sparse solutions when the objective involves a sparsity-inducing regularization. QuickeNing relies on limited-memory BFGS rules, making it appropriate for solving high-dimensional optimization problems. Besides, it enjoys a worst-case linear convergence rate for strongly convex problems. We present experimental results where QuickeNing gives significant improvements over competing methods for solving large-scale high-dimensional machine learning problems, see Figure 20 for example.

Catalyst Acceleration for First-order Convex Optimization: from Theory to Practice

Participants : Hongzhou Lin, Julien Mairal, Zaid Harchaoui [Univ. Washington] .

In [9], we introduce a generic scheme for accelerating gradient-based optimization methods in the sense of Nesterov. The approach, called Catalyst, builds upon the inexact accelerated proximal point algorithm for minimizing a convex objective function, and consists of approximately solving a sequence of well-chosen auxiliary problems, leading to faster convergence. One of the key to achieve acceleration in theory and in practice is to solve these sub-problems with appropriate accuracy by using the right stopping criterion and the right warm-start strategy. In this work, we give practical guidelines to use Catalyst and present a comprehensive theoretical analysis of its global complexity. We show that Catalyst applies to a large class of algorithms, including gradient descent, block coordinate descent, incremental algorithms such as SAG, SAGA, SDCA, SVRG, Finito/MISO, and their proximal variants. For all of these methods, we provide acceleration and explicit support for non-strongly convex objectives. We conclude with extensive experiments showing that acceleration is useful in practice, especially for ill-conditioned problems.

Catalyst Acceleration for Gradient-Based Non-Convex Optimization

Participants : Courtney Paquette [Univ. Washington] , Hongzhou Lin, Dmitriy Drusvyatskiy [Univ. Washington] , Julien Mairal, Zaid Harchaoui [Univ. Washington] .

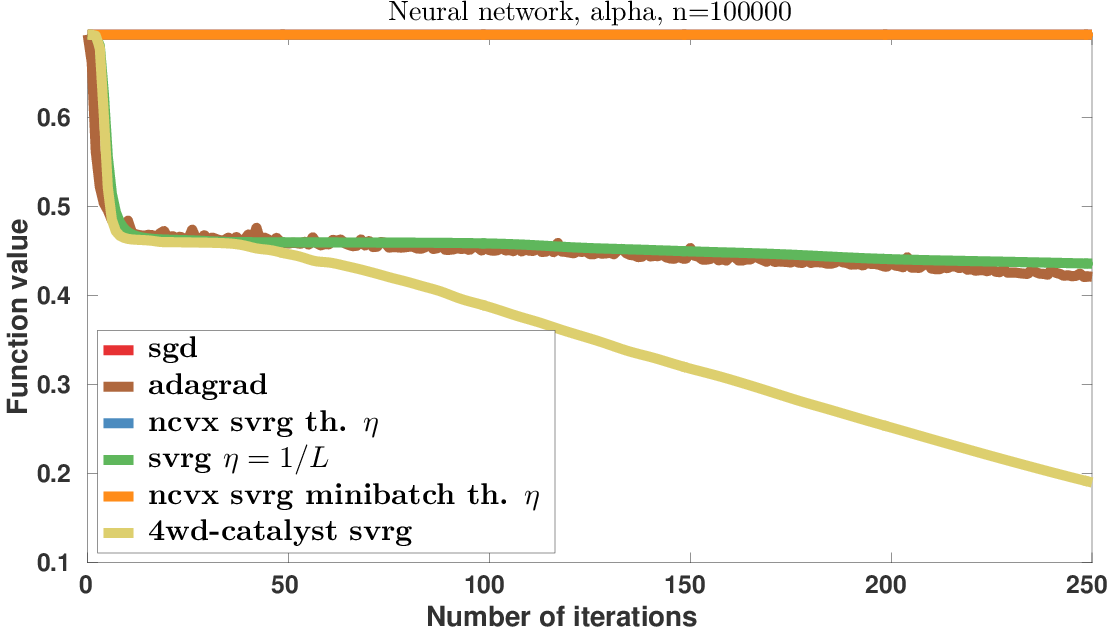
In [31], we introduce a generic scheme to solve nonconvex optimization problems using gradient-based algorithms originally designed for minimizing convex functions. When the objective is convex, the proposed approach enjoys the same properties as the Catalyst approach of Lin et al, 2015. When the objective is nonconvex, it achieves the best known convergence rate to stationary points for first-order methods. Specifically, the proposed algorithm does not require knowledge about the convexity of the objective; yet, it obtains an overall worst-case efficiency of $O\left({ϵ}^{-2}\right)$ and, if the function is convex, the complexity reduces to the near-optimal rate $O\left({ϵ}^{-2/3}\right)$. We conclude the paper by showing promising experimental results obtained by applying the proposed approach to SVRG and SAGA for sparse matrix factorization and for learning neural networks (see Figure 21).