Section: New Results

Computational Anatomy & Geometric Statistics

Riemannian Geometric Statistics in Medical Image Analysis

Participants : Xavier Pennec [Correspondant] , Stefan Sommer [CPH Univ, DK] , Tom Fletcher [University of Virginia at Charlottesville, USA] .

This work is partially funded by the ERC-Adv G-Statistics

Geometric statistics, Riemannian geometry, medical image analysis, computational anatomy

There has been a growing need in the medical image computing community for principled methods to process nonlinear geometric data. Riemannian geometry has emerged as one of the most powerful mathematical and computational frameworks for analyzing such data. In the book Riemannian Geometric Statistics in Medical Image Analysis [53], we provided an introduction to the core methodology for performing statistics on Riemannian manifolds and more general nonlinear spaces followed by a presentation of state-of-the-art methods in medical image analysis.

We provided more specifically an introduction chapter on differential and Riemannian geometry [56] (with S. Sommer and T. Fletcher), a comprehensive chapter on symmetric positive definite matrices (SPD) and manifold value image processing [55], and reference chapter on the affine connection setting for transformation groups including the stationary velocity fields parametrisation of diffeomorphisms and its use in medical image registration for longitudinal modeling of Alzheimer's disease [54] (with M. Lorenzi) and a chapter on the statistical bias on the estimation in quotient space [52] (with N. Miolane and L Devillier).

Effect of curvature on the Empirical Fréchet mean estimation in manifolds

Participant : Xavier Pennec [Correspondant] .

This work is funded by the ERC-Adv G-Statistics

Geometric statistics, empirical Fréchet mean

Statistical inference in manifolds most often rely on the Fréchet mean in the Riemannian case, or on exponential barycenters in affine connection spaces. The uncertainty of the empirical mean estimation with a fixed number of samples is a key question. In sufficient concentration conditions, a central limit theorem was established in Riemannian manifolds by Bhattacharya and Patrangenaru in 2005. We propose in [62] an asymptotic development valid in Riemannian and affine cases which better explain the role of the curvature in the modulation of the speed of convergence of the empirical mean. We also establish a non-asymptotic development in high concentration which shows a statistical bias on the empirical mean in the direction of the average gradient of the curvature. These curvature effects become important with large curvature and can drastically modify the estimation of the mean. They could partly explain the phenomenon of sticky means recently put into evidence in stratified spaces, notably in the case of negative curvature.

Shape Analysis with diffeomorphisms

Participants : Nicolas Guigui [Correspondant] , Shuman Jia, Maxime Sermesant, Xavier Pennec.

This work is partially funded by the ERC-Adv G-Statistics

Shape Analysis, parallel transport, LDDMM, symmetry

The statistical analysis of temporal deformations and inter-subject variability relies on shape registration and parallel transport of deformations (Figure 10). However, the numerical integration and optimization required lead to important numerical errors. This work aims at improving the numerical consistency and reproducibility of the Pole Ladder scheme to perform parallel transport. We propose a modification of this scheme using registration errors [39] and define different types of errors to evaluate the accuracy: the involutivity and transvectivity. We test our method on 138 cardiac shapes and demonstrate improved numerical consistency for both types of errors.

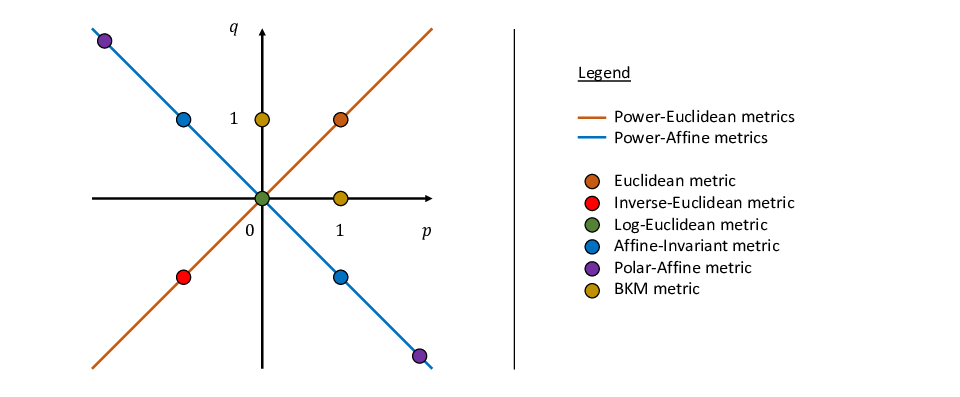
Classification of Riemannian metrics on the manifold of symmetric positive definite matrices

Participants : Yann Thanwerdas [Correspondant] , Xavier Pennec.

This work is partially funded by the ERC-Adv G-Statistics and by the IDEX UCA-JEDI ANR-15-IDEX-01 through an excellence OPhD fellowship.

Symmetric Positive Definite matrices, Riemannian metrics, dually flat manifolds

Symmetric Positive Definite matrices have been used in many fields of medical data analysis. Many Riemannian metrics have been defined on this manifold but the choice of the Riemannian structure lacks a set of principles that could lead one to choose properly the metric. We introduced several families of Riemannian metrics supported by a deformation principle and a principle of balanced metrics:

1. Power-Affine and Deformed-Affine metrics [43], that highlight relations between the affine-invariant, the polar-affine and the log-Euclidean metrics ;

2. Mixed-Power-Euclidean and Mixed-Power-Affine metrics [42], that highlight relations between many Riemannian metrics, as shown on Figure 11.

Statistical shape analysis of faces for computer aided dermatology and plastic surgery

Participants : Florent Jousse [Correspondant] , Xavier Pennec, Hervé Delingette, Matilde Gonzalez.

Supported by the company Quantificare through a CIFRE funding.

Gaussian Processes, non rigid registration

The objective of this work is to model complex face deformations related to natural aging, facial expressions, surgical interventions or posture motions to improve the 3D reconstruction of faces and to normalize their analysis. It includes the development of non-rigid registration methods of textured meshes and their statistical modeling through Gaussian processes.

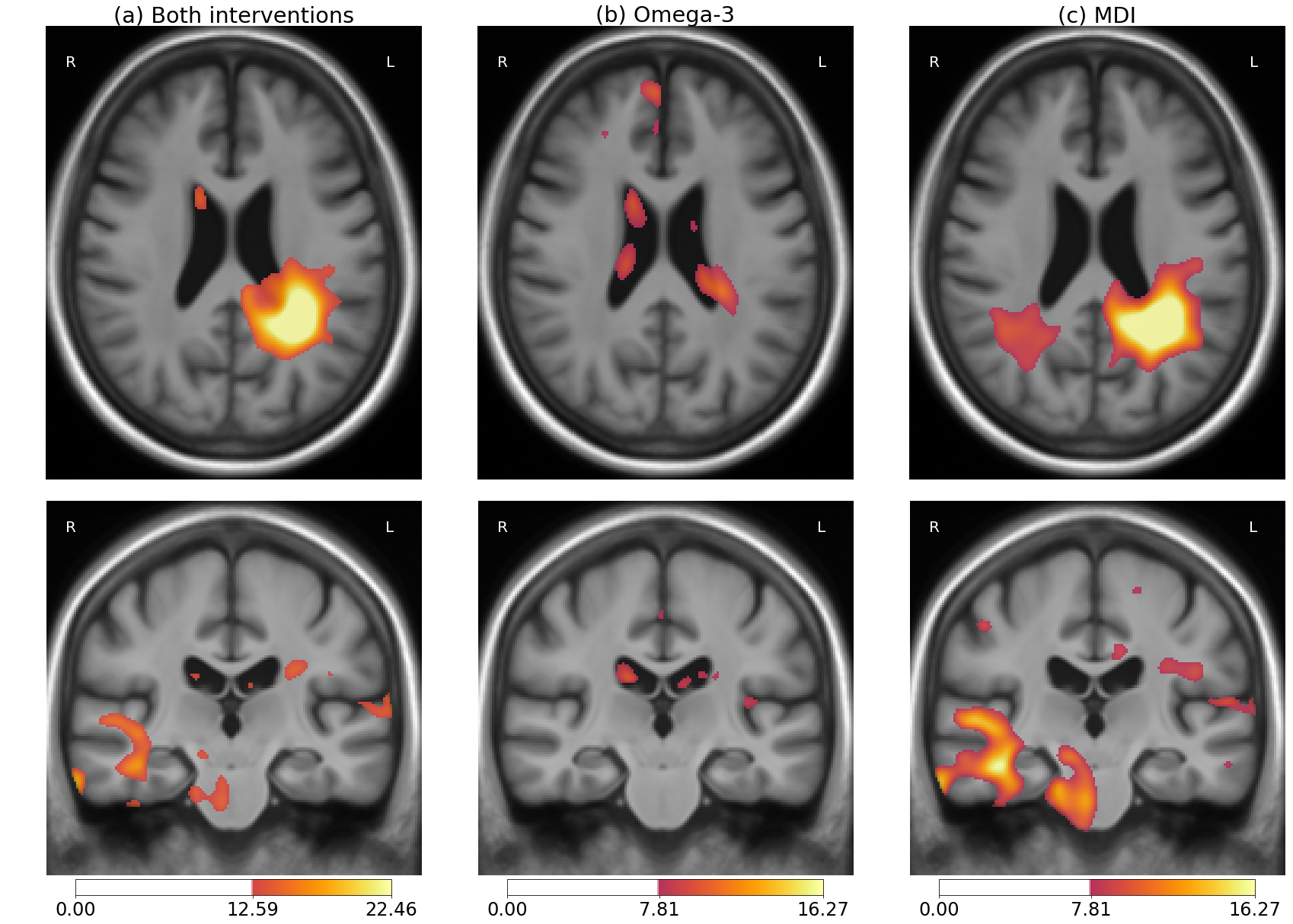
Brain Morphometry in the MAPT clinical trial

Participants : Raphaël Sivera [Correspondant] , Hervé Delingette, Marco Lorenzi, Xavier Pennec, Nicholas Ayache.

This work is partially funded by the ERC-Adv G-Statistics

Longitudinal deformation modeling, multivariate statistics, brain morphology, Alzheimer's disease, clinical trial.

• We proposed a complete framework for statistical hypothesis testing on mass-multivariate data. This framework builds on the recent works on multivariate statistics in neuroimaging to propose a generic approach adapted to the study of longitudinal deformations [3].

• This framework is used in the context of the MAPT study to highlight a significant effect of the multidomain intervention on the brain morphological changes (see Figure 13) [22].

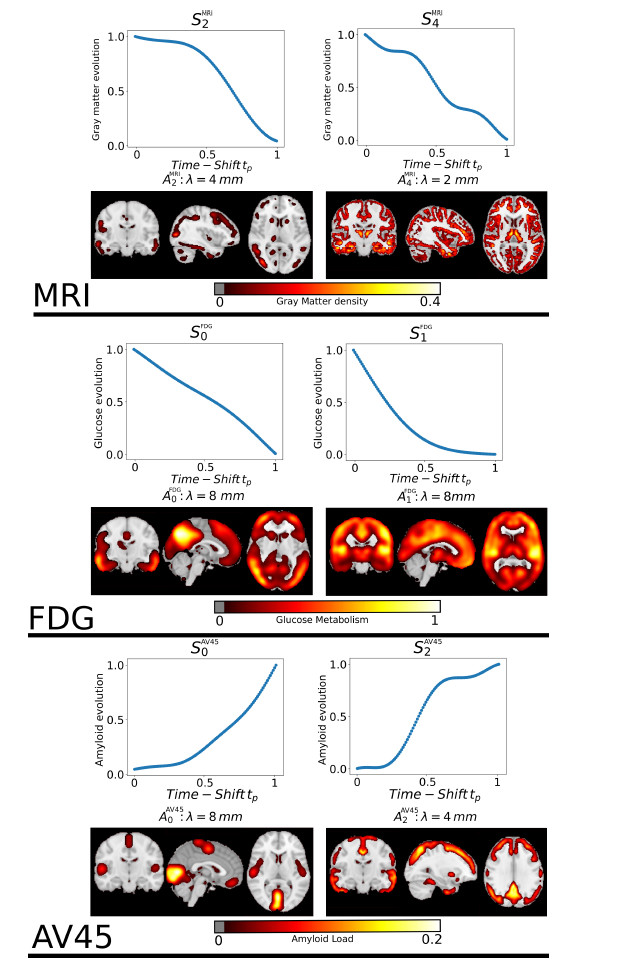
Statistical Learning of Heterogeneous Data in Large-Scale Clinical Databases

Participants : Clement Abi Nader [Correspondant] , Nicholas Ayache, Philippe Robert, Marco Lorenzi.

Gaussian Process, Alzheimer's Disease, Disease Progression Modelling

The aim of this thesis is to develop a spatio-temporal model of Alzheimer's Disease (AD) progession based on multi-modal brain data. We assume that the brain progression is characterized by independent spatio-temporal sources that we want to separate. We estimate brain structures involved in the disease progression at different resolutions thus dealing with the non-stationarity of medical images, while assigning to each of them a monotonic temporal progression using Gaussian processes (Figure 14). We also compute an individual time-shift parameter to assess the disease stage of each subject. This work has been accepted for publication in the journal NeuroImage [5]