Section: New Results

Automated Discovery in Self-Organizing Systems

Curiosity-driven Learning for Automated Discovery of Physico-Chemical Structures

Participants : Chris Reinke [correspondant] , Mayalen Etcheverry, Pierre-Yves Oudeyer.

Introduction

Intrinsically motivated goal exploration algorithms (IMGEPs) enable machines to discover repertoires of action policies that produce a diversity of effects in complex environments. In robotics, these exploration algorithms have been shown to allow real world robots to acquire skills such as tool use [81] [55]. In other domains such as chemistry and physics, they open the possibility to automate the discovery of novel chemical or physical structures produced by complex dynamical systems [134]. However, they have so far assumed that self-generated goals are sampled in a specifically engineered feature space, limiting their autonomy. Recent work has shown how unsupervised deep learning approaches could be used to learn goal space representations [136] but they have used precollected data to learn the representations. This project studies how IMGEPs can be extended and used for automated discovery of behaviours of dynamical systems in physics or chemistry without using assumptions or knowledge about such systems.

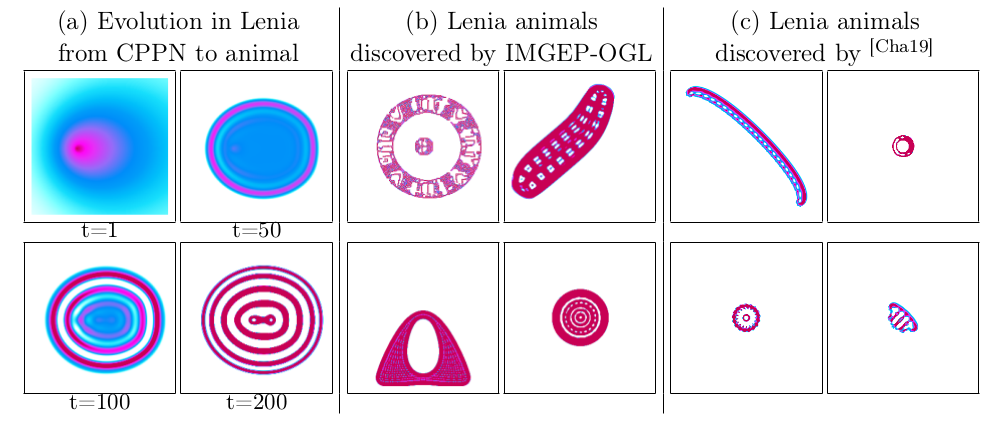
As a first step towards this goal we choose Lenia [66], a simulated high-dimensional complex dynamical system, as a target system. Lenia is a continuous cellular automaton where diverse visual structures can self-organize (Fig.17, c). It consists of a two-dimensional grid of cells $A\in {[0,1]}^{256\times 256}$ where the state of each cell is a real-valued scalar activity $A^t\left(x\right)\in [0,1]$. The state of cells evolves over discrete time steps $t$. The activity change is computed by integrating the activity of neighbouring cells. Lenia's behavior is controlled by its initial pattern $A^{t=1}$ and several settings that control the dynamics of the activity change. Lenia can produce diverse patterns with different dynamics. Most interesting, spatially localized coherent patterns that resemble in their shapes microscopic animals can emerge. Our goal was to develop methods that allow to explore a high diversity of such animal patterns.

We could successfully accomplish this goal [30] based on two key contributions of our research: 1) the usage of compositional pattern producing networks (CPPNs) for the generation of initial states for Lenia, and 2) the development of a novel IMGEP algorithm that learns goal representations online during the exploration of the system.

1) CPPNs for the generation of initial states

A key role in the generation of patterns in dynamical systems is their initial state $A^{t=1}$. IMGEPs sample these initial states and apply random perturbations to them during the exploration. For Lenia this state is a two-dimensional grid with $256\times 256$ cells. Performing directly a random sampling of the $256\times 256$ grid cells results in initial patterns that resemble white noise. Such random states result mainly in the emergence of global patterns that spread over the whole state space, complicating the search for spatially localized patterns. We solved the sampling problem for the initial states by using compositional pattern producing networks (CPPNs) [148]. CPPNs are recurrent neural networks that allow the generation of structured initial states (Fig.17, a). The CPPNs are used as part of the system parameters which are explored by the algorithms. They are defined by their network structure (number of neurons, connections between neurons) and their connection weights. They include a mechanism for random mutation of the weights and structure.

2) IMGEP for Online Learning of Goal Space Representations

We proposed an online goal space learning IMGEP (IMGEP-OGL), which learns the goal space incrementally during the exploration process. A variational autoencoder (VAE) is used to encode Lenia patterns into a 8-dimensional latent representation used as goal space. The training procedure of the VAE is integrated in the goal sampling exploration process by first initializing the VAE with random weights. The VAE network is then trained every $K$ explorations for $E$ epochs on the previously idetnfied patterns during the exploration.

Experiments

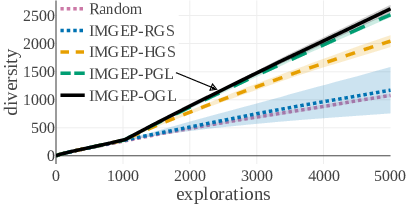
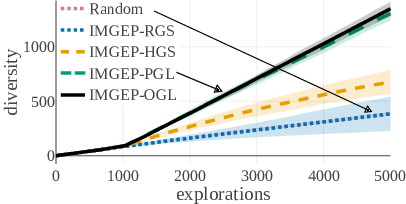
We evaluated the performance of the novel IMGEP-OGL to other exploration algorithms by comparing the diversity of their identified patterns. Diversity is measured by the spread of the exploration in an analytic behavior space. This space is defined by a latent representation space that was build through the training of a VAE to learn the important features over a very large dataset of Lenia patterns identified during the many experiments over all evaluated algorithms. We then augmented that space by concatenating hand-defined features. Each identified Lenia pattern is represented by a specific point in this space. The space was then discretized in a fixed number of areas/bins of equal size. The final diversity measure of each algorithm is the number of areas/bins in which at least one explored pattern exists.

We compared different exploration algorithms to the novel IMGEP-OGL: 1) Random exploration of system parameters, 2) IMGEP-HGS: IMGEP with a hand-defined goal space, 3) IMGEP-PGL: IMGEP with a learned goal space via an VAE by a precollected dataset of Lenia patterns, and 4) IMGEP-RGS: IMGEP with a VAE with random weights that defines the goal space.

The system parameters $\theta$ consisted of a CPPN that generates the initial state $A^{t=1}$ for Lenia and 6 further settings defining Lenia's dynamics: $\theta =[\mathrm{CPPN}\to A^{t=1},R,T,\mu ,\sigma ,{\beta }_1,{\beta }_2,{\beta }_3]$. The CPPNs were initialized and mutated by a random process that defines their structure and connection weights as done. The random initialization of the other Lenia settings was done by an uniform distribution and their mutation by a Gaussian distribution around the original values.

Results

The diversity of identified patterns in the analytic behavior space show that IMGEP approaches with learned goal spaces via VAEs (PGL, OGL) could identify the highest diversity of patterns overall (Fig. 18, a). They were followed by the IMGEP with a hand-defined goal space (HGS). The lowest performance had the random exploration and the IMGEP with a random goal space (RGS). The advantage of learned goals space approaches (PGL, OGL) over all other approaches was even stronger for the diversity of animal patterns, i.e. the main goal of our exploration (Fig. 18, b).

Conclusion

Our goal was to investigate new techniques based on intrinsically motivated goal exploration for the automated discovery of patterns and behaviors in complex dynamical systems. We introduced a new algorithm (IMGEP-OGL) which is capable of learning unsupervised goal space representations during the exploration of an unknown system. Our results for Lenia, a high-dimensional complex dynamical system, show its superior performance over hand-defined goal spaces or random exploration. It shows the same performance as a learned goal space based on precollected data, showing that such a precollection of data is not necessary. We furthermore introduced the usage of CPPNs for the successful initialization of the intial states of the dynamical systems. Both advances allowed us to explore an unknown and high-dimensional dynamical system which shares many similarities with different physical or chemical systems.