Section: New Results

Approximation

Cost-driven framework for progressive compression of textured meshes

Participants : Cédric Portaneri, Pierre Alliez.

In collaboration with Michael Hemmer (Google X), Lukas Birklein and Elmar Schoemer (Uni. of Mainz).

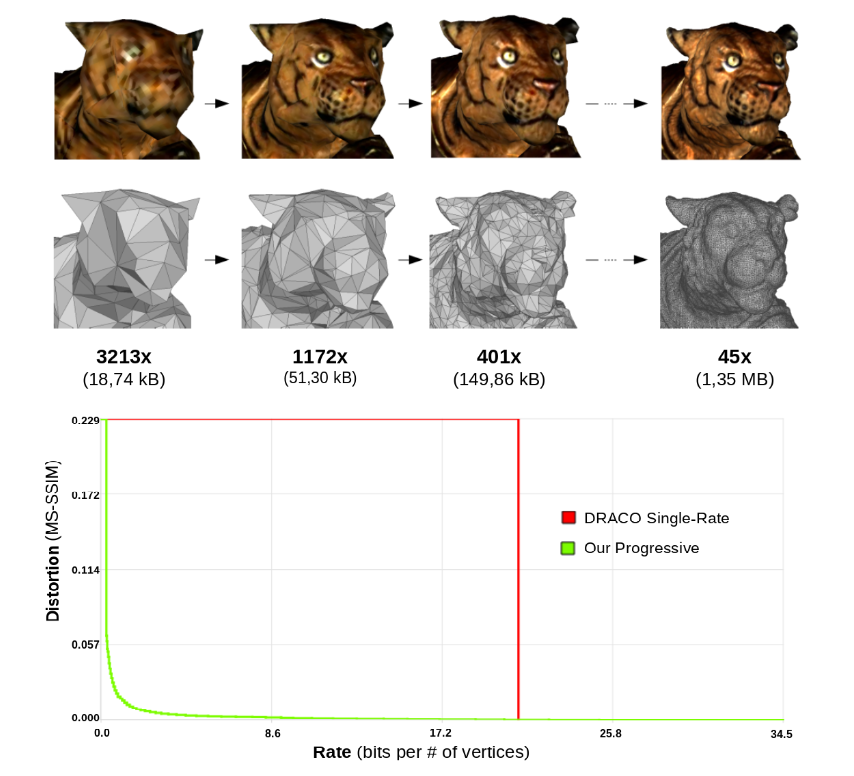
Recent advances in digitization of geometry and radiometry generate in routine massive amounts of surface meshes with texture or color attributes. This large amount of data can be compressed using a progressive approach which provides at decoding low complexity levels of details (LoDs) that are continuously refined until retrieving the original model. The goal of such a progressive mesh compression algorithm is to improve the overall quality of the transmission for the user, by optimizing the rate-distortion trade-off. In this paper, we introduce a novel meaningful measure for the cost of a progressive transmission of a textured mesh by observing that the rate-distortion curve is in fact a staircase, which enables an effective comparison and optimization of progressive transmissions in the first place. We contribute a novel generic framework which utilizes the cost function to encode triangle surface meshes via multiplexing several geometry reduction steps (mesh decimation via half-edge or full-edge collapse operators, xyz quantization reduction and uv quantization reduction). This framework can also deal with textures by multiplexing an additional texture reduction step. We also design a texture atlas that enables us to preserve texture seams during decimation while not impairing the quality of resulting LODs. For encoding the inverse mesh decimation steps we further contribute a significant improvement over the state-of-the-art in terms of rate-distortion performance and yields a compression-rate of 22:1, on average. Finally, we propose a unique single-rate alternative solution using a selection scheme of a subset among LODs, optimized for our cost function, and provided with our atlas that enables interleaved progressive texture refinements (see Figure 7). This work was presented at the ACM Multimedia Systems conference [19] and obtained the best paper award.

Selective padding for Polycube-based hexahedral meshing

Participant : Pierre Alliez.

In collaboration with Gianmarco Cherchi and Riccardo Scateni from University of Cagliari (Sardinia), Max Lyon from University of Aachen and David Bommes from University of Bern.

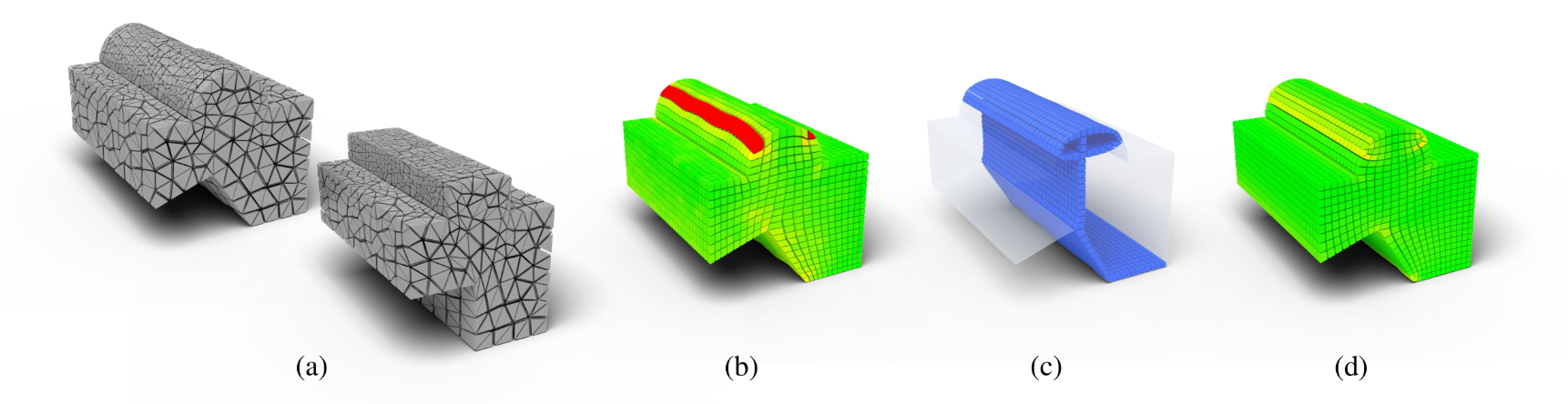
Hexahedral meshes generated from polycube mapping often exhibit a low number of singularities but also poor quality elements located near the surface. It is thus necessary to improve the overall mesh quality, in terms of the minimum Scaled Jacobian (MSJ) or average Scaled Jacobian (ASJ). Improving the quality may be obtained via global padding (or pillowing), which pushes the singularities inside by adding an extra layer of hexahedra on the entire domain boundary. Such a global padding operation suffers from a large increase of complexity, with unnecessary hexahedra added. In addition, the quality of elements near the boundary may decrease. We propose a novel optimization method which inserts sheets of hexahedra so as to perform selective padding, where it is most needed for improving the mesh quality. A sheet can pad part of the domain boundary, traverse the domain and form singularities. Our global formulation, based on solving a binary problem, enables us to control the balance between quality improvement, increase of complexity and number of singularities. We show in a series of experiments that our approach increases the MSJ value and preserves (or even improves) the ASJ, while adding fewer hexahedra than global padding. (See Figure 8). This work was published in an international journal and was presented at the EUROGRAPHICS conference [4].