EN FR
EN FR


previous Previous | up Home | Next next


Section: New Results

Reconstruction

City Reconstruction from Airborne Lidar: A Computational Geometry Approach

Participants : Jean-Philippe Bauchet, Florent Lafarge.

Figure 5. City Reconstruction from Airborne Lidar. Our method consists of three main steps. We first label points of the LiDAR scan as ground, vegetation or roof. Then, we apply a contouring algorithm to the height map, revealing the facades initially absent in the point set. Finally, we extract and propagate planar primitives from the point cloud, dividing the space into polyhedra that are labeled to obtain a 3D reconstruction of buildings.
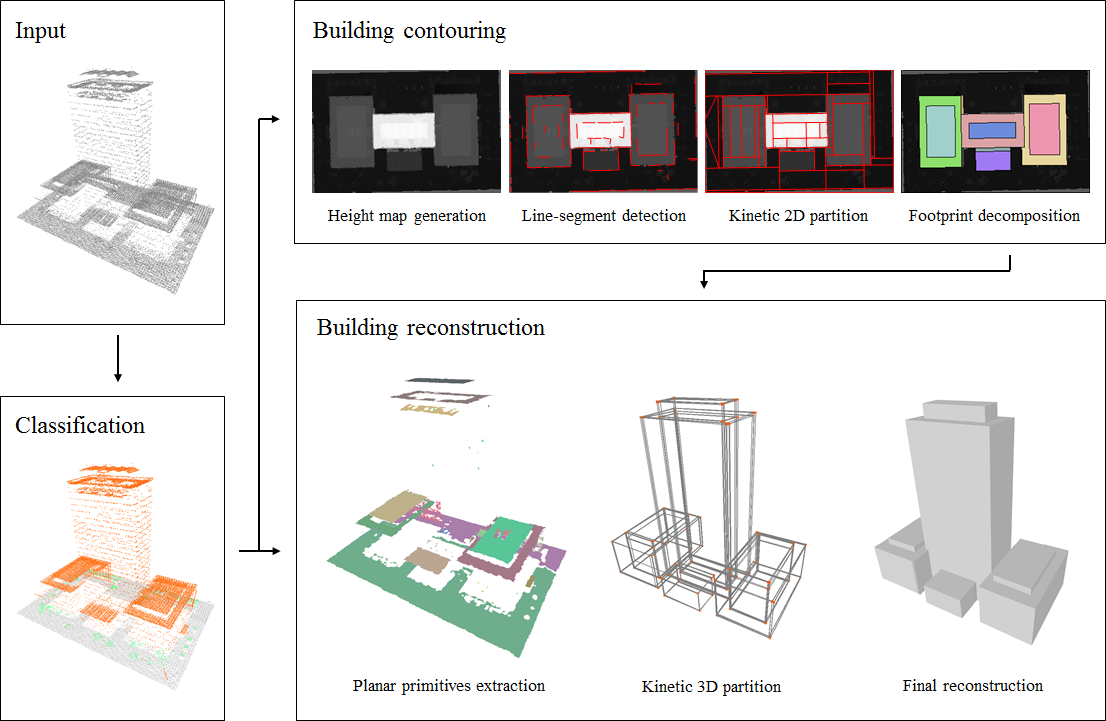
IMG/geoinfo19.png

We introduce a pipeline that reconstructs buildings of urban environments as concise polygonal meshes from airborne LiDAR scans. It consists of three main steps: classification, building contouring, and building reconstruction, the two last steps being achieved using computational geometry tools. Our algorithm demonstrates its robustness, flexibility and scalability by producing accurate and compact 3D models over large and varied urban areas in a few minutes only (See Figure 5). This work was published in the ISPRS international conference 3D GeoInfo [14].

Extracting geometric structures in images with Delaunay point processes

Participant : Florent Lafarge.

In collaboration with Jean-Dominique Favreau (Ekinnox), Adrien Bousseau (GraphDeco Inria team) and Alex Auvolat (Wide Inria team).

We introduce Delaunay Point Processes, a framework for the extraction of geometric structures from images. Our approach simultaneously locates and groups geometric primitives (line segments, triangles) to form extended structures (line networks, polygons) for a variety of image analysis tasks. Similarly to traditional point processes, our approach uses Markov Chain Monte Carlo to minimize an energy that balances fidelity to the input image data with geometric priors on the output structures. However, while existing point processes struggle to model structures composed of interconnected components, we propose to embed the point process into a Delaunay triangulation, which provides high-quality connectivity by construction. We further leverage key properties of the Delaunay triangulation to devise a fast Markov Chain Monte Carlo sampler. We demonstrate the flexibility of our approach on a variety of applications, including line network extraction, object contouring, and mesh-based image compression (See Figure 6). This work was published in the IEEE journal TPAMI [7].

Figure 6. Example applications of Delaunay Point Processes to extract planar graphs representing blood vessels in retina images (left), and complex polygons representing object silhouettes (right). The point distribution creates a dynamic Delaunay triangulation while edge and facet labels specify the geometric structure (see red edges on close-ups).
IMG/pami19.png


previous Previous | up Home | Next next