Section: New Results

Biological imagery

Regularizing parameter estimation with Poisson noise

Participants : Mikael Carlavan, Laure Blanc-Féraud [contact] .

The problem is to automatically estimate the regularizing parameter in Poisson noisy image deconvolution using the $L_1$-norm regularization as a total variation or frame coefficients. This problem is addressed using the discrepancy principle. The standard weighted criterion composed of a data term and a regularization term is rewritten as a constrained minimization problem. The constraint is designed on the data term using the discrepancy principle and a new estimation of the bound is proposed as well as an efficient algorithm to solve this constrained minimization problem. This work is published in [10] , [24] , [9] .

Brain vascular network segmentation

Participant : Xavier Descombes [contact] .

This work was conducted in collaboration with Franck Plouraboué and Abdelhakim El Boustani from IMFT Toulouse and Caroline Fonta from CerCo Toulouse. It has been partially supported by a PEP II project from CNRS.

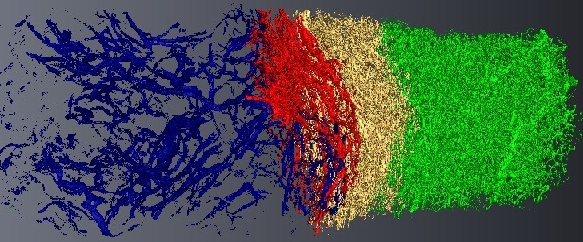
Micro-tomography produces high resolution images of biological structures such as vascular networks. We have proposed a new approach for segmenting vascular network into pathological and normal regions from considering their micro-vessel 3D structure only. We consider a partition of the volume obtained by a watershed algorithm based on the distance from the nearest vessel. Each region is characterized by its volume and the local vascular density. The volume and density maps are first regularized by minimizing the total variation. Then, a new approach has been proposed to segment the volume from the two previous restored images based on hypothesis testing. Results are presented on 3D micro-tomographic images of the brain micro-vascular network (see Fig. 16 ).

Figure 16. Brain micro-vascular network segmentation

Blind restoration of 3D biological image

Participants : Saima Ben Hadj, Laure Blanc-Féraud [contact] .

Fluorescence microscopy is a powerful imaging technique providing three-dimensional images of biological living specimen. However, these images are degraded by a depth variant blur due to light diffraction phenomenon as well as refractive index mismatch between the different mediums composing the system and the biological sample. They are also distorted with noise from non-ideal imaging conditions. In order to provide biologist with more suitable images for quantitative studies, many restoration methods were developed. In most of them, the blur function, called Point Spread Function (PSF) is assumed to be piecewise constant in order to avoid the intensive computing time when using a pointwise varying PSF. However, this usually leads to blocking effect in the restored image. In our work, we extend the Space varying (SV) blur model previously proposed in [39] for 2D astronomical images to 3D microscopy images. In that model, the degraded image is a convex combination of convolutions with a space-invariant (SI) PSF. Furthermore, we fit to that model two restoration procedures which are basically developed for a SI PSF. On the one hand, we use the Richardson-Lucy method with Total Variation regularization which is carried out under Poisson noise assumption in order to restore confocal microscopy images. We employ another method with total variation regularization adapted to images with an additive Gaussian noise in order to restore Wide Field Microscopy images. For that, we rely on a fast optimization method based on a domain-decomposition technique [36] . In particular, we study its convergence properties when using the SV blur model [31] , [27] . To illustrate the interest of the proposed method, we show in Fig 17 some results obtained on a simulated bead image of Wide Field Microscopy.

Figure 17. (X,Z) slices of the (a) original image, (b) degraded image (c) restored image using a SV blur model, and (d) restored image with a space-invariant PSF.

(a) (b) (c) (d)

Axon imaging

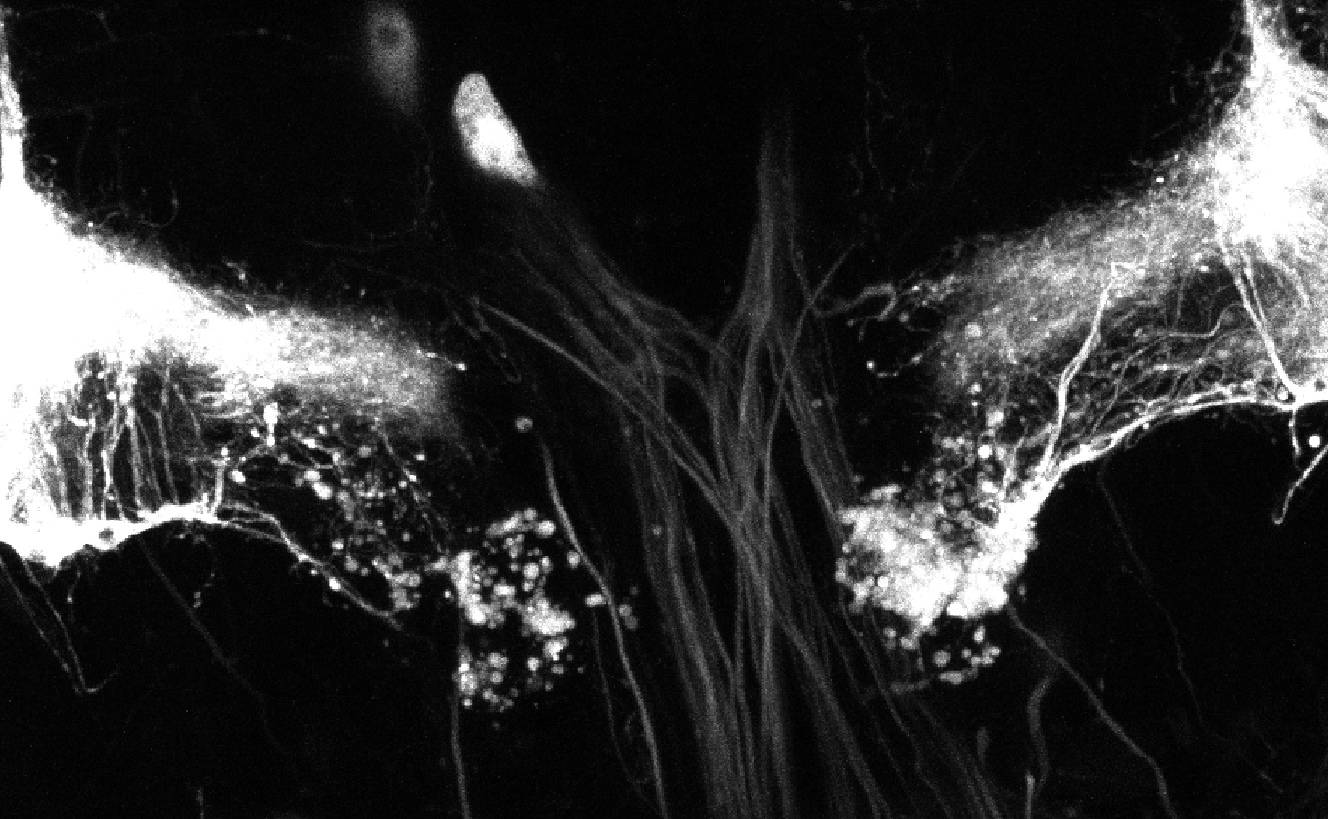
Participant : Florence Besse [contact] .

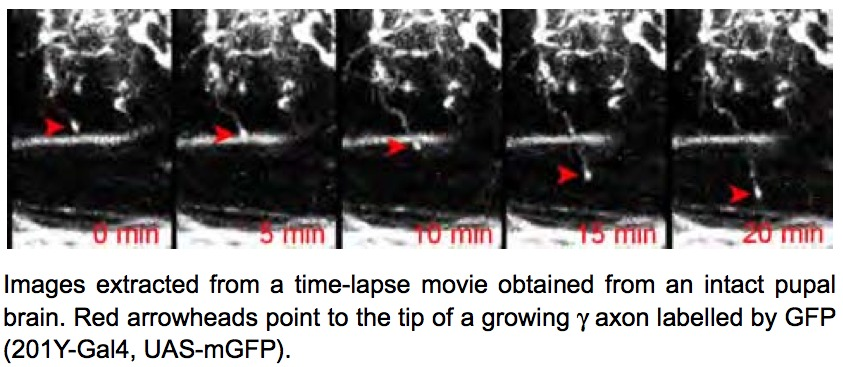
During brain development, neurons extend cellular processes (dendrites and axons) to connect to specific targets and establish functional networks. Understanding how axonal processes migrate to reach their targets and how they form new branches to build up a complex axonal tree is thus key. To characterize the properties of axonal trees, we have generated a collection of confocal 3D pictures of normal and mutant single axons labeled using a fluorescent protein. To analyze the formation of axonal trees in real-time, we have developed a protocol to dynamically image growing axons within intact Drosophila brains. In this protocol, entire brains are cultured in conditions where they can undergo cell differentiation and maturation. Axons are labeled by the fluorescent molecule GFP and are imaged over 12h, with very low-photobleaching and no associated phototoxicity, using an ultra-sensitive 2-photon microscope. Several image sequences corresponding to the growth of axons in normal conditions have been acquired (see Fig.  18 ).

Figure 18. Axon growth imaging

Detection of Axons in Neuronal Images

Participants : Alejandro Mottini, Florence Besse, Xavier Descombes [contact] .

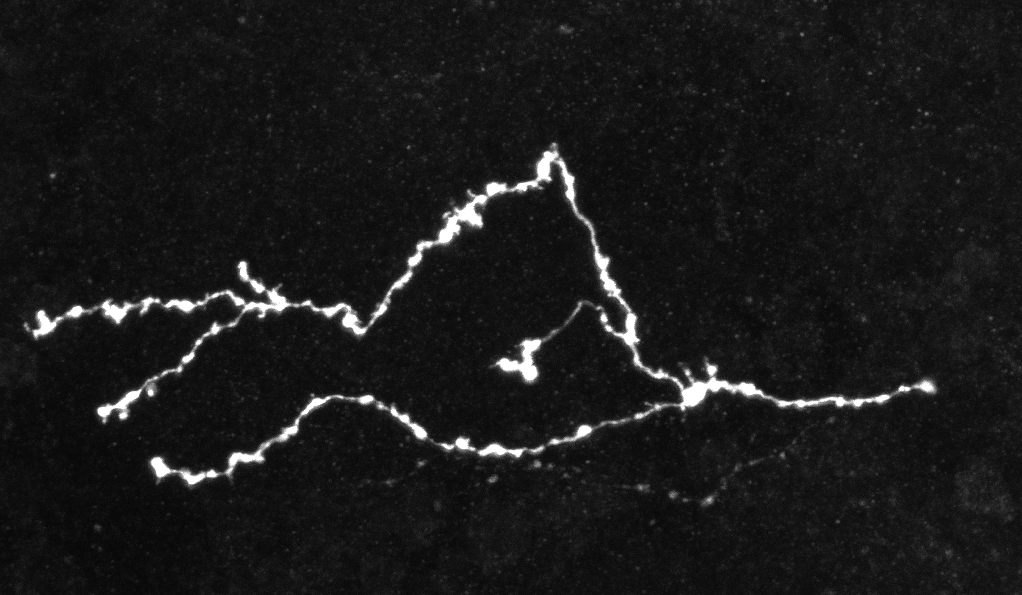
Imaging techniques such as confocal and two-photon microscopy provide an efficient way of analyzing supra-cellular structures. It is known that the precise shape of these objects provides information on their functioning and allows the characterization of pathological states. Therefore, the analysis of the morphological differences between normal and pathological structures is of paramount importance. In particular, the analysis of neuronal axon topologies allows biologists to study the causes of neurological diseases such as Fragile X Syndrome and Alzheimer's disease. For this purpose biologists have acquired static 3D images of mature neuron axons using fluorescent confocal microscopy.

Figure 19. Static axon images (2D maximum intensity projection).

Due to the high volume of generated image data and the tortuous nature of the axons, manual processing is infeasible. Therefore, it is necessary to develop techniques for the automatic extraction and analysis of the neuronal structures. However, since both types of images present different characteristics, two different methodologies need to be developed. The main objective of the static case is the study of the length and number of bifurcation points of the two populations of neurons. On the other hand, the focus in the dynamic case is put on the tracking of the axonal tips. The automatic extraction of axons from confocal microscope images is a key problem in the field of neuron axon analysis. In this work we propose a solution which combines algorithms for the denoising, binarization, skeletonization, gap filling, point detection and statistical analysis in a pipeline capable of extracting the axons. Furthermore, these algorithms were incorporated in a software, developed in Matlab, which includes an easy to use GUI along with functionalities to facilitate high data throughput analysis. The software was evaluated on several 3D confocal microscope images of normal and mutated axons. Our results support the potential use of the software in helping biologist perform automatic morphological analysis of axons in fluorescent confocal microscopy images.

Figure 20. Original (left) and extracted (right) normal axon image (2D maximum intensity projection).

Axons tracking

Participants : Alejandro Mottini, Huei-Fang Yang, Florence Besse, Xavier Descombes [contact] .

This work was funded by project ARC-DADA (INRIA/CNRS/UNSA) [http://www-sop.inria.fr/members/Xavier.Descombes/DADA/home.html ]. It is done in collaboration with Serpico team at INRIA Bretagne (C. Kervrann, P. Houllier)

To study axon growth process biologists have acquired dynamic 3D+t image sequences of developing neurons using fluorescent two-photon microscopy.

Figure 21. Dynamic images (2D maximum intensity projection).

Live cell two-photon microscopy is an effective tool for the analysis of dynamical processes occurring in living samples that, when combined with fluorescence, allows the detection of objects of interest in 3D space and time. These labeled objects appear as bright spots which need to be detected. The low resolution and signal-to-noise-ratio (SNR) make this analysis difficult even for experienced biologists. As a consequence, automatic detection techniques need to be robust and flexible. To this end, the Marked Point Process (MPP) detection framework was selected. Since axonal extremities appear either as circular objects or as ending points of thin filaments, we proposed two different MPP models. These models were formulated using a Gibbs energy function and optimized with Multiple Births and Deaths, a newly proposed algorithm which guarantees a fast convergence to the global minimum. The first model is designed to detect spheres or disks and the second filaments (both in 3D). Both models were tested on several 3D static images. To evaluate the performance of the detection, results were compared against images labeled by an experienced biologist.

Figure 22. Original (left) and resulting (right) images (detected disks in pink). The true axonal tip is circled in white (original image) and red (result). In the original image, axons are labeled in white.

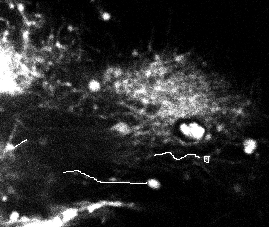
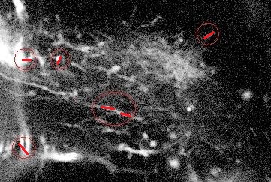
Figure 22 shows the results obtained on one frame of a video sequence (the shown image is a slice of the 3D frame) for the disk/sphere model. One can appreciate that the axonal tip marked by the biologist (in white, left) was detected. However, a false positive is also present.

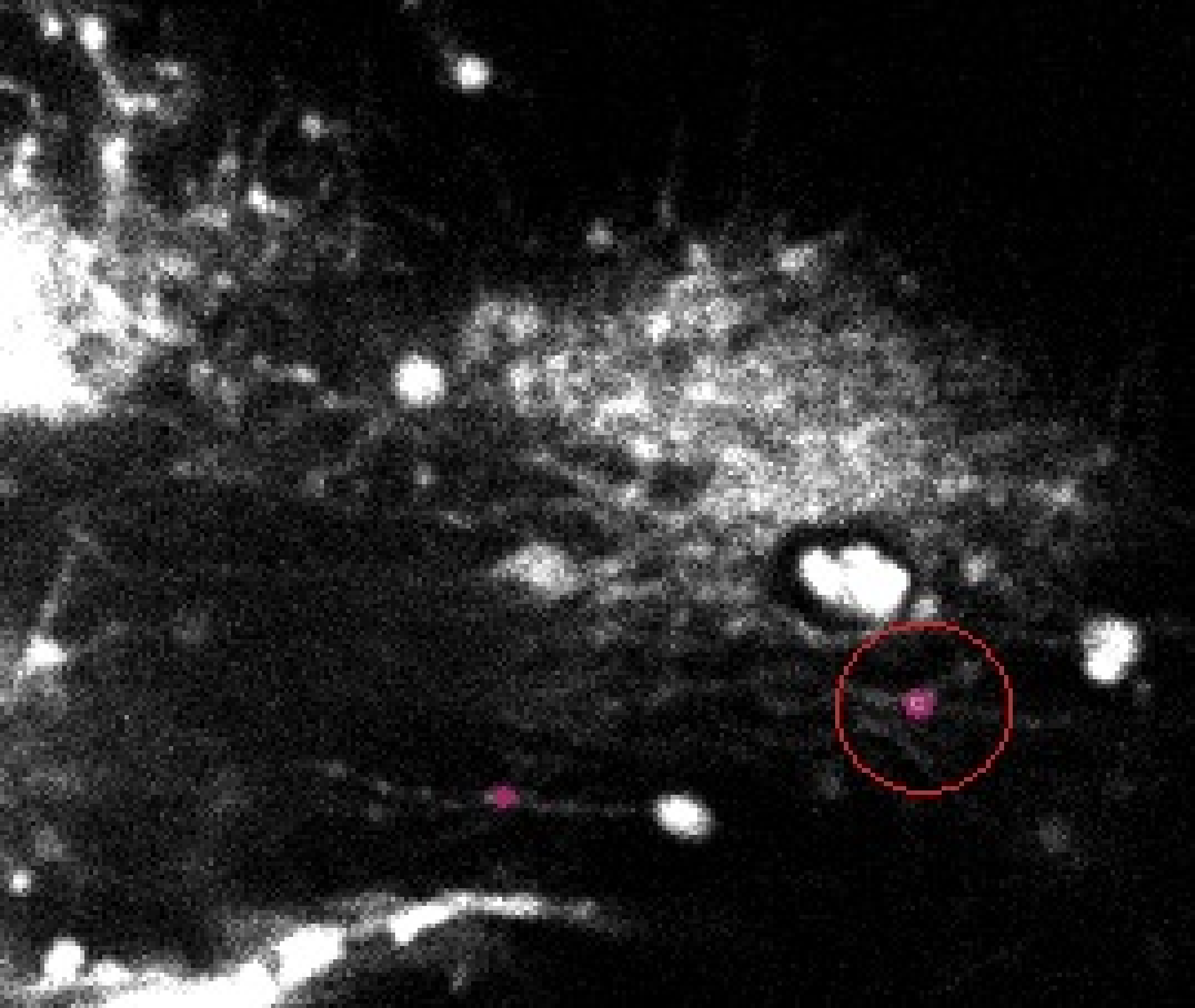
Figure  23 shows the result obtained on one of the slices (for the same video frame) for the filament model. Although the good filament was detected, many false positives are also present in the image. Similar results where obtained for other images.

Figure 23. Original image (left) (targeted filament circled in red) and result (right) (detected filaments in red, circled in red).

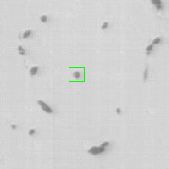
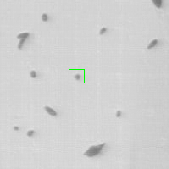
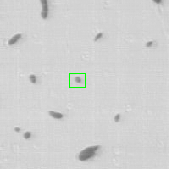
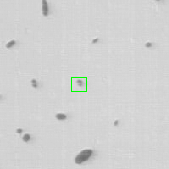
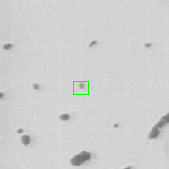
Once the detection of the extremities in each frame of the video has been solved, the solution should be embedded into a tracking algorithm to obtain an estimation of the axon's trajectory during the growing stage. To this end, the particle filtering technique was considered. This technique consists in estimating the posterior distribution of the current state $x_t$ of the target of interest at time $t$ based on the measurements $z_{1..t}$ :

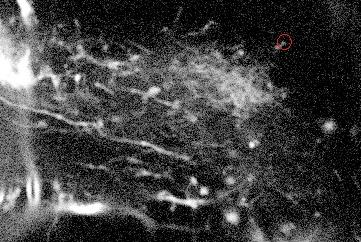
where $p\left(x_t|x_{t-1}\right)$ is the transition distribution, and $p\left(z_t|x_t\right)$ is the likelihood. In the current implementation, a simple kinematic model is used for the transition distribution, and a color histogram is applied to the computation of the likelihood. Figure 24 shows the preliminary results obtained by applying the particle filtering technique on the coronal KESM (Knife-Edge Scanning Microscopy) sections of the mouse cerebellum, where the green rectangles indicate the tracked objects.

Figure 24. Tracking results on the coronal KESM sections of the mouse cerebellum. The green rectangles are the tracked objects. The user gives an initial starting region on the first image, and the algorithm tracks the region of interest in the subsequent images. Note that the images are cropped for a better view.

The next step will be to design a more sophisticated transition distribution and likelihood model that are suitable for tracking the trajectories of axons during their growth.