Section: New Results

Approximation

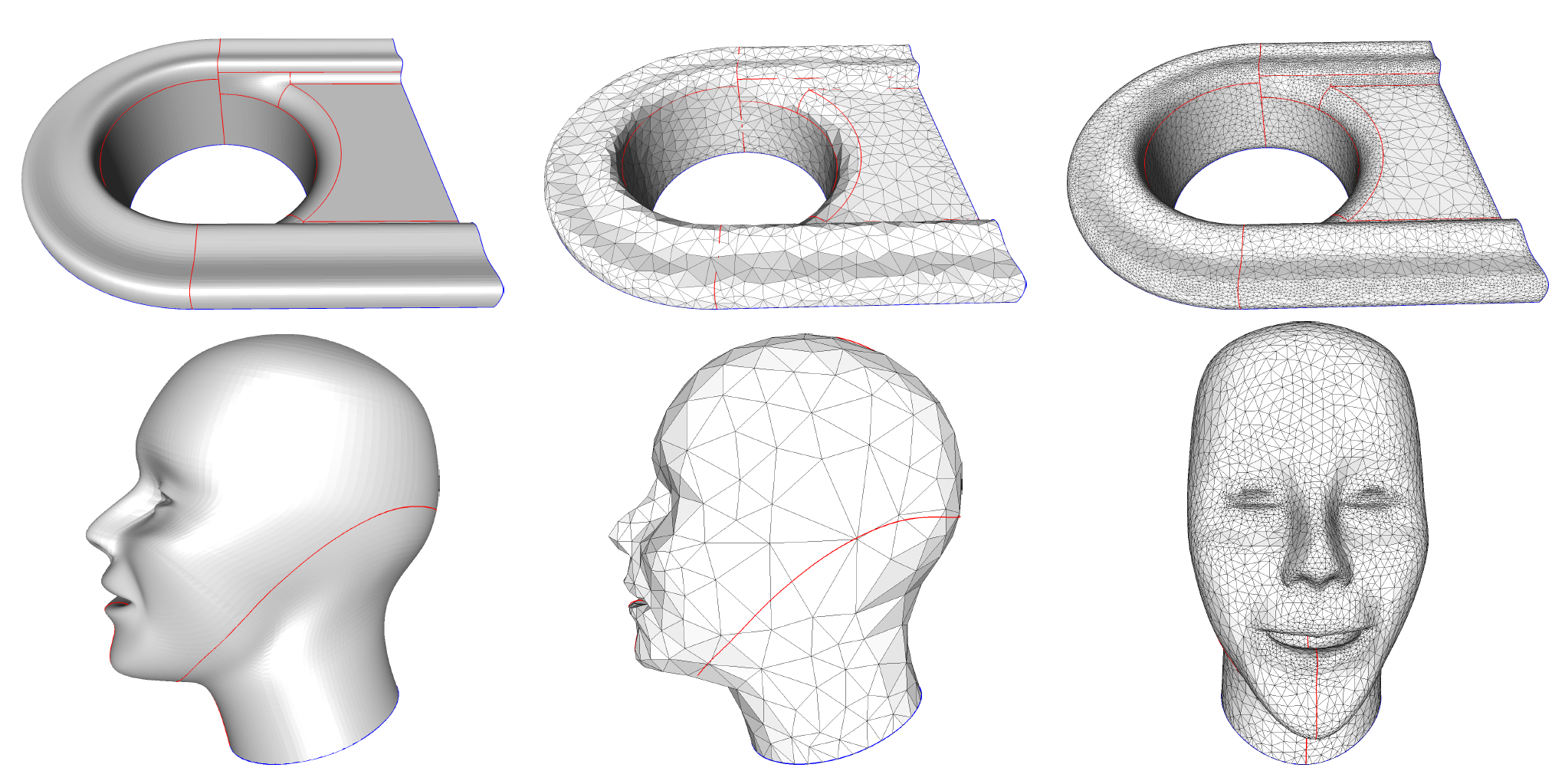
A Line/Trimmed NURBS Surface Intersection Algorithm Using Matrix Representations

Participant : Pierre Alliez.

In collaboration with Laurent Busé from Inria AROMATH, and Jingjing Shen and Neil Dodgson from Cambridge University (UK).

We contribute a reliable line/surface intersection method for trimmed NURBS surfaces, based on a novel matrix-based implicit representation and numerical methods in linear algebra such as singular value decomposition and the computation of generalized eigenvalues and eigenvectors. A careful treatment of degenerate cases makes our approach robust to intersection points with multiple pre-images. We then apply our intersection algorithm to seamlessly mesh NURBS surfaces through Delaunay refinement (see Figure 8). We demonstrate the added value of our approach in terms of accuracy and treatment of degenerate cases, by providing comparisons with other intersection approaches as well as a variety of meshing experiments. This work was published in Computer Aided Geometric Design [6].

Optimal Voronoi Tessellations with Hessian-based Anisotropy

Participants : Pierre Alliez, Mathieu Desbrun.

In collaboration with Max Budninskiy and Beibei Liu from Caltech, Fernando de Goes from Pixar and Yiying Tong from Michigan State University.

We contribute a variational method to generate cell complexes with local anisotropy conforming to the Hessian of any given convex function and for any given local mesh density. Our formulation builds upon approximation theory to offer an anisotropic extension of Centroidal Voronoi Tessellations which can be seen as a dual form of Optimal Delaunay Triangulation. We thus refer to the resulting anisotropic polytopal meshes as Optimal Voronoi Tessellations. Our approach sharply contrasts with previous anisotropic versions of Voronoi diagrams as it employs first-type Bregman diagrams, a generalization of power diagrams where sites are augmented with not only a scalar-valued weight but also a vector-valued shift. As such, our OVT meshes contain only convex cells with straight edges (Figure 9), and admit an embedded dual triangulation that is combinatorially-regular. We show the effectiveness of our technique using off-the-shelf computational geometry libraries. This work was published at ACM SIGGRAPH Asia [3].

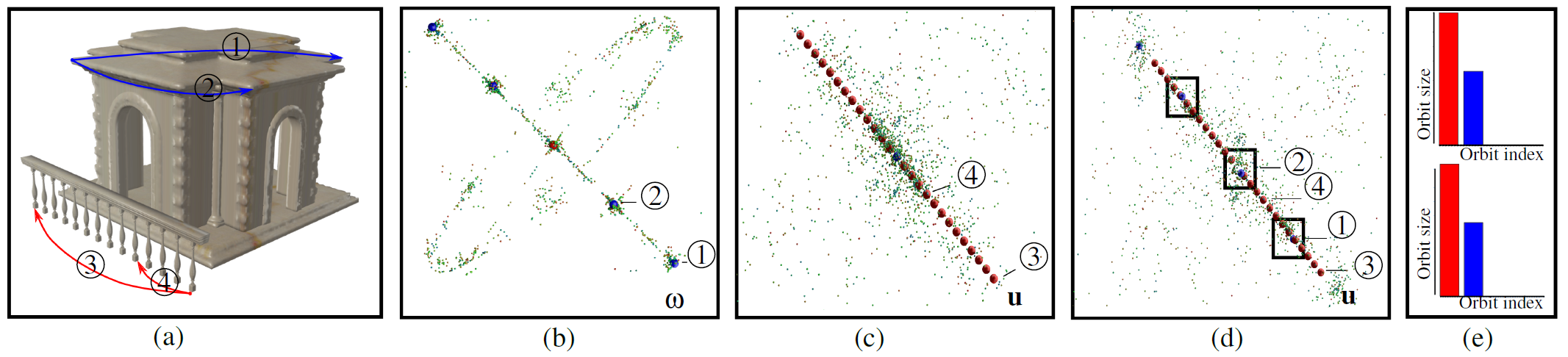
Symmetry and Orbit Detection via Lie-Algebra Voting

Participants : Pierre Alliez, Mathieu Desbrun.

In collaboration with Zeyun Shi, Hujun Bao and Jin Huang from Zhejiang University.

We formulate an automatic approach to the detection of partial, local, and global symmetries and orbits in arbitrary 3D datasets. We improve upon existing voting-based symmetry detection techniques by leveraging the Lie group structure of geometric transformations. In particular, we introduce a logarithmic mapping that ensures that orbits are mapped to linear subspaces, hence unifying and extending many existing mappings in a single Lie-algebra voting formulation (Figure 10). Compared to previous work, our resulting method offers significantly improved robustness as it guarantees that our symmetry detection of an input model is frame, scale, and reflection invariant. As a consequence, we demonstrate that our approach efficiently and reliably discovers symmetries and orbits of geometric datasets without requiring heavy parameter tuning. This work was published in the proceedings of the EUROGRAPHICS Symposium on Geometry Processing [7].